탐욕 알고리즘(Greedy Algorithm)이란?
최적의 해에 가까운 값을 구하기 위해 사용되는 알고리즘이다.
가장 큰 특징은 여러 경우 중 하나를 결정해야할 때마다, 매 순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행하여 최종적인 값을 구하는 방식을 말한다.
특징 자체가 구현 방식을 말하는 것이기에 예제를 통해 바로 알아보겠다.
예제1) 동전 문제
Q1. 지불해야 하는 값이 4720일 때, 1원, 50원, 100원, 500원 동전으로 동전의 수가 가장 적게 지불하게끔 구현해보아라.
Java 코드 구현
public class GreedyCoin {
public static void main(String[] args) {
//4720을 500,100, 50, 10 동전으로 최소한의 개수 구하기
ArrayList<Integer> coinList = new ArrayList<Integer>(Arrays.asList(500,100,50,10));
ArrayList<Integer> details = new ArrayList<Integer>();
int price = 4720;
int totalCoinCount = 0;
int coinNum = 0;
for(int i=0; i< coinList.size(); i ++){
coinNum = price / coinList.get(i); // 몫 = 동전 개수
totalCoinCount += coinNum; // 토탈 동전 개수
price -= coinNum * coinList.get(i); // 몫 * 금액하여 나머지 대입
details.add(coinNum);
System.out.println(coinList.get(i) + "원: " + coinNum + "개");
}
System.out.println("총 동전 갯수:" + totalCoinCount);
}
}
코드 구현 설명
- 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식으로 구현 가능
- 탐욕 알고리즘으로 매 순간 최적이라고 생각되는 경우를 선택하면 됨
예제2) 부분 배낭(Fractional Knapsack Problem) 문제
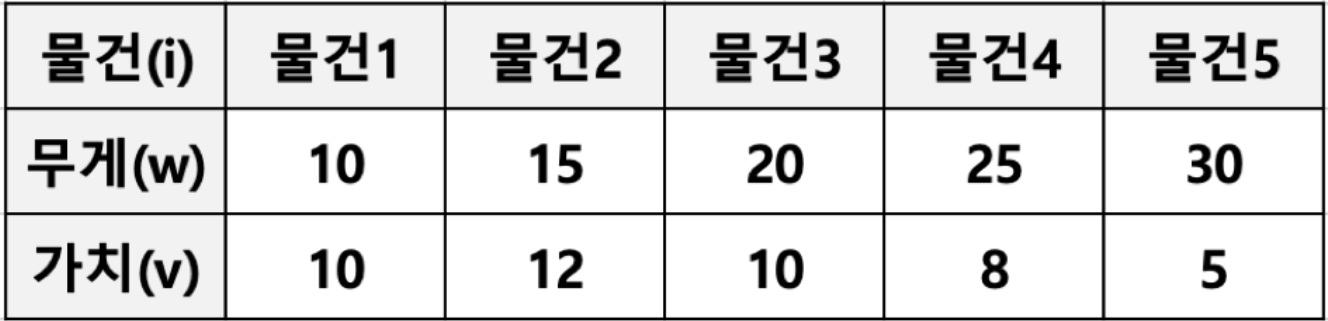
Q2. 무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣어보아라.
- 각 물건은 무게(w)와 가치(v)로 표현될 수 있다.
- 물건은 쪼갤 수 있으므로 물건의 일부분이 배낭에 넣어질 수 있다.
Java 코드 구현
//무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣는문제
public class GreedyKnapsack {
public static void main(String[] args) {
int[][] objectList = { {10,10}, {15,12},{20,10},{25,8},{30,5}};
knapsackFunc(objectList, 30.0);
}
private static void knapsackFunc(int[][] objectList, double capacity){
double totalValue = 0.0;
double fraction = 0.0;
//objectList Sort
Arrays.sort(objectList, new Comparator<int[]>() {
@Override
public int compare(int[] obj1, int[] obj2) {
return ((obj2[1] / obj2[0]) - (obj1[1] / obj1[0]));
}
});
for(int i = 0; i<objectList.length; i++){
//if(배낭 무게 - 리스트 무게 > 0)
if(capacity - (double) objectList[i][0] > 0){
capacity -= (double) objectList[i][0];
//리스트 가치 더하기
totalValue += (double) objectList[i][1];
System.out.println("무게:" + objectList[i][0] + ", 가치:" + objectList[i][1]);
}else{// 쪼개서 배낭에 넣기
fraction = capacity / (double) objectList[i][0];
totalValue += (double) objectList[i][1] * fraction;
System.out.println("무게:" + objectList[i][0] + ",가치:" + objectList[i][1] + ", 비율:" + fraction);
break;
}
}
System.out.println("총 담을 수 있는 가치 : " + totalValue);
}
}코드 구현 설명
- objectList에 무게와 가치를 2차원 배열 설정
- 배낭 무게(capacity) : 30.0 설정
- Comparator를 사용하여 가장 큰 무게를 기준으로 정렬
- 배낭 무게 - 리스트 무게가 크다면
- capacity에서 빼주고 총 가치(totalValue)에 가치를 추가
- 배낭 무게 - 리스트 무게가 작다면
- 무게를 쪼개서 배낭에 넣어준다.
- 쪼갠 비율 = 무게 / 물건의 무게
- 배낭 무게 - 리스트 무게가 크다면
- Comparator를 사용하여 가장 큰 무게를 기준으로 정렬
- 총 담을 수 있는 가치를 출력
탐욕 알고리즘의 한계?
- 보통 탐욕 알고리즘은 근사치 추정에 활용한다.
- 반드시 최적의 해를 구할 수 있는 것은 아니기 때문이다.
- 최적의 해에 가까운 값을 구하는 방법중의 하나이다.
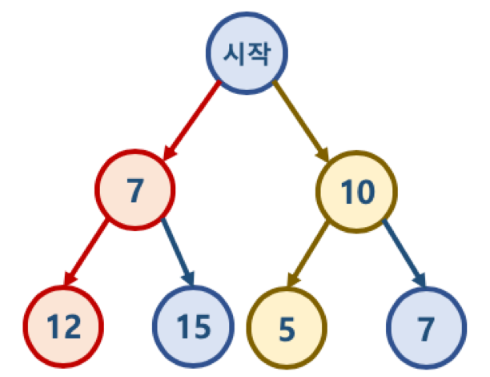
위의 이미지를 예시로 최적의 해를 구할 수 없다는 것을 이해해보자.
- 시작 노드에서 시작하여 가장 작은 값을 찾아 leaf node까지 가는 경로를 찾는다 가정.
- 탐욕 알고리즘 적용 시 시작 -> 7 -> 12를 선택하게 되므로 7 + 12 = 19
- 하지만 실제 가장 작은 값은 시작 -> 10 -> 5, 10 + 5 = 15이다.
- 따라서 탐욕 알고리즘을 사용하여 최적의 해를 찾는데는 무리가 있을 수 있다는 것을 확인할 수 있다.
반응형
'Algorithm > Concept' 카테고리의 다른 글
| [Java] 너비 우선 탐색(BFS), 깊이 우선 탐색(DFS)이란? (개념 /코드 예제) (0) | 2022.07.14 |
|---|---|
| [Java] 순차 탐색, 이진 탐색의 개념과 예제 (0) | 2022.07.13 |
| [Java] 고급 정렬 - 퀵 정렬이란? (개념 / 예제 / 알고리즘 분석) (0) | 2022.07.13 |
| [Java] 고급 정렬 - 병합 정렬이란? (개념/ 예제/ 총 정리) (3) | 2022.07.12 |
| [Java] 동적 계획법과 분할 정복이란? (개념/ 공통점/ 차이점/ 예제) (0) | 2022.07.12 |


댓글